MergeSort(병합정렬)-알고리즘06
2023. 8. 13. 16:47ㆍCS(Computer Science)/Algorithm
MergeSort(병합정렬)
분할정복(devide and conquer)이라는 알고리즘 설계 패러다임을 이용한 대표적인 알고리즘이다.
즉, 어떤 문제(problems)를 재귀적으로 분할해 나가서 subproblems(부분문제?)들을 이용해 문제를 해결하고 다시 합치는 개념이다.
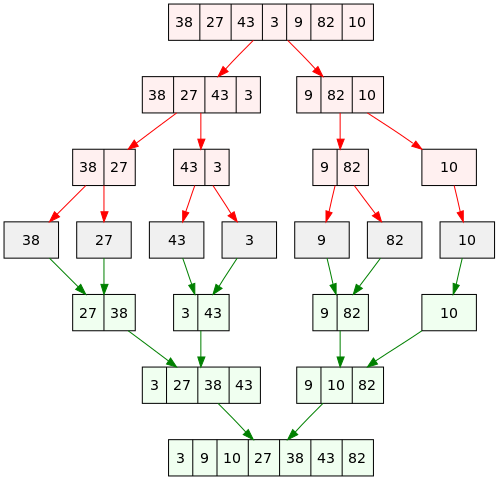
다음 사진에서 빨간부분이 분할단계, 초록부분이 합치는 단계이다. 분할을 해서 값을 비교하여 정렬하고 다시 합치는 로직이다.
알고리즘
- 정렬할 데이터의 크기가 0 또는 1이면 이미 정렬 된 것으로 본다. (사진에서 회색부분)
- 크기가 2 이상이면 반으로 쪼갠다.
- 1~2반복...(빨간색 부분)
- 원래 같은 집합에서 나온 데이터 집합 둘을 합치는데 정렬 순서를 맞춰서 합친다.(초록색 부분)
- 4 반복
시간복잡도
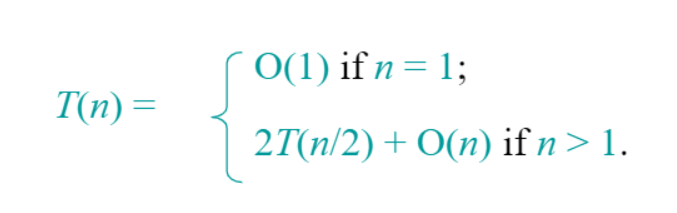
병합정렬을 재귀식으로 나타내면 위 식과 같다.
$2T(\frac{n}{2})$은 재귀적으로 데이터를 절반으로 분할,(1~3 과정)
$O(n)$는 각 데이터 집합을 합치는 것을 나타낸다.(4~5)과정.
따라서 병합정렬의 시간복잡도는 O(nlog₂n) 이 된다. (재귀트리, 마스터메서드 이용)
코드 구현(C)
void MergeSort(int arr[], int left, int right) {
if(left==right) return;
int mid;
mid = (left + right) / 2; //분할의 기준점
MergeSort(arr, left, mid); //분할(좌측)
MergeSort(arr, mid + 1, right); //분할(우측)
Merge(arr, left, right); //합병 함수
}void Merge(int arr[], int p, int q, int r) {
int i = p, j = q+1, k = p;
int tmp[원래 배열의 크기]; // 새 배열
while(i<=q && j<=r) {
if(data[i] <= data[j]) tmp[k++] = data[i++];
else tmp[k++] = data[j++];
}
while(i<=q) tmp[k++] = data[i++];
while(j<=r) tmp[k++] = data[j++];
for(int a = p; a<=r; a++) data[a] = tmp[a];
}합병 함수(맨처음 사진에서의 초록부분)에서는 새로운 배열을 만들고 거기에 합병 결과값을 넣은 다음 다시 원래 배열에 복붙한다.
ex) [3] + [1] --> tmp:[1,3]--->arr:[1,3]
장단점
단점:
- Not inplace: 위의 코드의 Merge함수를 보면 알겠지만, 추가적인 메모리가 필요하다.(새로운 배열 생성)
- 데이터의 이동횟수가 많으므로 데이터의 크기가 클 때 효율적이지 않다.
장점:
- 언제나 O(nlog₂n)의 시간복잡도를 보장한다.
- Stable: 같은 값을 비교할때, 그 순서를 유지한다. ex) [2] + [2'] --> [2,2']
'CS(Computer Science) > Algorithm' 카테고리의 다른 글
| DynamicProgramming(DP)-알고리즘08 (0) | 2023.08.20 |
|---|---|
| 기본 정렬 알고리즘(선택,삽입)-알고리즘07 (0) | 2023.08.15 |
| Worst-Case Linear-Time Selection(+퀵정렬)-알고리즘05 (0) | 2023.07.13 |
| QuickSort(2)-알고리즘04 (0) | 2023.06.30 |
| QuickSort(1)-알고리즘03 (0) | 2023.06.18 |