막대 자르기(DP)-알고리즘09

 

막대 자르기(Rod cut algorithm)

 

길이가 n인 막대와 i = 1,2,3,...,n에 대한 가격 $ p_{i} $의 표가 주어지면 해당 막대를 잘라서 판매했을떄 얻을 수 있는 최대수익 $r_{n}$을 결정한다. 길이가 n인 막대의 가격 $p_{n}$이 충분히 비싸면 최적해는 자르지 않은 것일 수도 있다.

 

아래 예시를 보자.

n=4 일 때, 위의 그림은 길이가 4인 막대를 자르는 방법을 모두 보여준다. 길이 4의 막대를 길이 2의 막대 두개로 나누면 최적의 수익으로 $ p_{2} $ + $ p_{2} $ = 5 + 5 = 10 이 발생함을 알 수 있다.

 

 

 

 

브루트포스

 

 

길이가 n인 막대는 $2^{n-1}$ 개의 다른 방법으로 나눌 수 있는데 제일 왼쪽에서 부터 i = 1,2,3,...,n-1 에 대한 모든 i길이마다 자르거나 자르지 않거나 하는 독립적인 선택이 가능하기 때문이다.

 

따라서 모든 경우의 수를 따져보는 브루트포스 알고리즘으로 이 문제를 해결하면 O($2^{n}$)의 시간이 걸린다.

 

 

 

 

동적 프로그래밍(DP)

 

 

만약 최적해가 막대를 1$\leq$k$\leq$n 에 대하여 k개의 조각으로 나눈다고 하면,

막대를 조각 길이 $ i_{1} $ $ i_{2} $ $ i_{3} $ ... $ i_{k} $로 나누는 최적의 분해는 

다음과 같은 최대의 수익을 제공한다.

$ r_{n} $ = $ p_{i_{1}} $ + $ p_{i_{2}} $ + ... + $ p_{i_{k}} $ 

 

이를 일반적으로 표현하면,

 

$r_{n}$ = max( $p_{n}$   ,   $r_{1}$ + $r_{n-1}$  ,   $r_{2}$ + $r_{n-2}$   , ...,  $r_{n-1}$ + $r_{1}$ )

 

첫번째 인자 $p_{n}$은 자르지 않고 길이가 n인 막대를 그대로 파는 것에 해당한다.

max에 대한 나머지 인자는 막대를 맨 처음에 i = 1,2,...,n-1에 대해 길이 i 와 길이 n-i가 되게 둘ㄹ 나누고 두 조각을 더 최적으로 잘라 두 조각으로 부터 $r_{i}$와 $r_{n-i}$의 수익을 얻는 것 중에서 얻어진 최대 수익에 해당한다.

 

즉, 크기가 n인 막대의 최대수익을 얻기 위해 크기가 n-r,r 인 막대의 최대수익을 얻는다.

(=전체적인 최적해는 두 부분 문제의 각각에 대해 수익을 최대화하는 해를 이용한다)

 

따라서 막대 자르기 문제는 최적 부분 구조(Optimal substructure)를 가졌다고 한다.

 

 

 

다음의 더 간단한 공식도 얻을 수 있다.

 

 

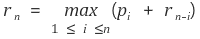
동적 프로그래밍으로 이를 구현하는 방법으로 메모이제이션이 있다.

부분 문제를 해결했을 때 배열이나 해시테이블에 저장해 놓았다가 이를 이용하도록 한다.

 

Memoized_cut_rod(p,n)
{
	r[0...n]을 새로운 배열이라 한다.
    for i=0 to n:
		r[i]=-inf
    return memoized(p,n,r)
}

memoized(p,n,r)
{
	if r[n]>=0
    	return r[n]
    if n==0:
    	q=0
    else 
    	q=-inf
        
        
        **************************************
    	for i = 1 to n:    
        	q = max(q,p[i]+memoized(p,n-i,r))
        **************************************
        
        
    r[n]=q
    return q
}

***표시를 해놓은 부분이

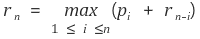
를 표현한 부분이다.