Solving Recurrences-알고리즘02
재귀함수의 식을 예로 다음을 볼 수 있다.

이러한 재귀식은 알고리즘을 분석할 때, 특히 recursive algorithm을 분석 할때 많이 쓰인다
예를 들면 n!을 구하는 알고리즘의 T(n)은 어떻게 구할까?
f(n)=n!
이라고 할때
f(n)=f(n-1)*n=f(n-2)*(n-1)*(n) .... 이다.
f(n)의 연산횟수를 T(n)이라고 한다면
T(n)
= T(n-1) + 1 (f(n-1)과 n의 곱셈)
= T(n-2) + 1 (f(n-2)와f(n-1)의 곱셈) + 1 이므로
따라서 f(n) = O(n) 이다.

그렇다면 이런식은 어떻게 풀까?
이런 복잡한 식들을 푸는 방법 3가지를 오늘 알아보자.
1. Substitution Method
귀납적 풀이랑 비슷하다.(이산수학에서나오는 것과 똑같은 거 같다)
이 풀이는 거의 3가지 과정으로 나뉜다.
수업시간에는 다음 3가지 과정으로 배웠다
- Guess the form of the solution
- Verify by induction
- Solve for constants
먼저 T(n)이 O(g(n))이라고 가정을 한다. 즉 T(n) ≥ c·g(n) for all n≥n0 ifor certain c.
그리고 수학적 귀납법을 이용해 가정이 참임을 증명하고 BaseCase에 대해서 참임을 보여주면 된다. 예시로 한 문제를 풀어보자.
다음은 Binary Search 의 time complexity를 구하는 과정이다.
T(n) = d + T(n/2)
Guess: T(n) = O(logn)
Induction goal : T(n) ≤ c·logn for some c and n≥n0
Inductive hypothesis: T(n/2) ≤ c·log(n/2)
Proof of Induction goal:
T(n) = T(n/2) + d ≤ c·log(n/2) + d
= c·logn - c + d ≤ c·logn (since -c + d ≤ 0 when c ≥ d) 귀납법으로 증명완료
BaseCase: T(n) = θ(1) for all n<n0
therefore T(n) = O(logn) .
하나 더 풀어보자
T(n) = 2T(√n) + logn
이런 문제는 m=logn 이라고 두고 치환을 한다.
풀이 :

2. Recursive Tree(재귀트리)
사실 위의 substitution method는 직관적으로 수식을 보고 guess단계를 위해 추측을 해야 그 추측에 대한 증명을 할 수 있는데 보통 추측을 tight하게 하기가 쉽지않다. 이 recursive tree는 그런것에 활용이 된다.

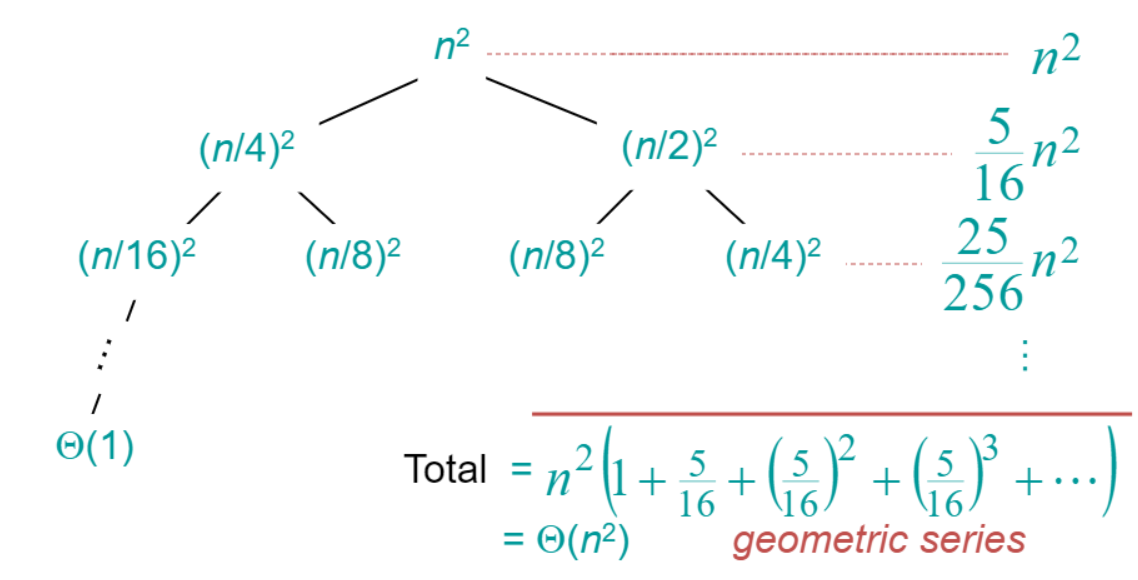
다음 식을 재귀트리로 표현해보자. 트리의 각 level에서 소요되는 시간(여기서는 n^2)들을 모두 더하면 된다.


T(n) --->

---->

--->
3. Master Method
마스터 방법은 수행시간 식이 다음과 같은 형태를 띄거나 다음의 형태로 변환 가능한 경우에만 사용할 수 있다.

3가지 경우에 따라 그냥 공식을 때려 박으면 된다.
Case1:$f(n) = O(n^{ log_{b} a- \varepsilon } ) $ for some $\varepsilon > 0$ , then $T(n) = \Theta (log_{b} a) $
Case2:$f(n) = \Theta (n^{ log_{b} a } ) $, then $T(n) = \Theta (log_{b} a) $
Case3:$f(n) = \Omega (n^{ log_{b} a+\varepsilon } ) $ for some $\varepsilon > 0$ , then $T(n) = \Theta (log_{b} a) $
and if
$f(n/b) ≤ cf(n) $ for some c < 1 and all sufficiently large n, then $T(n) = \Theta(f(n))$